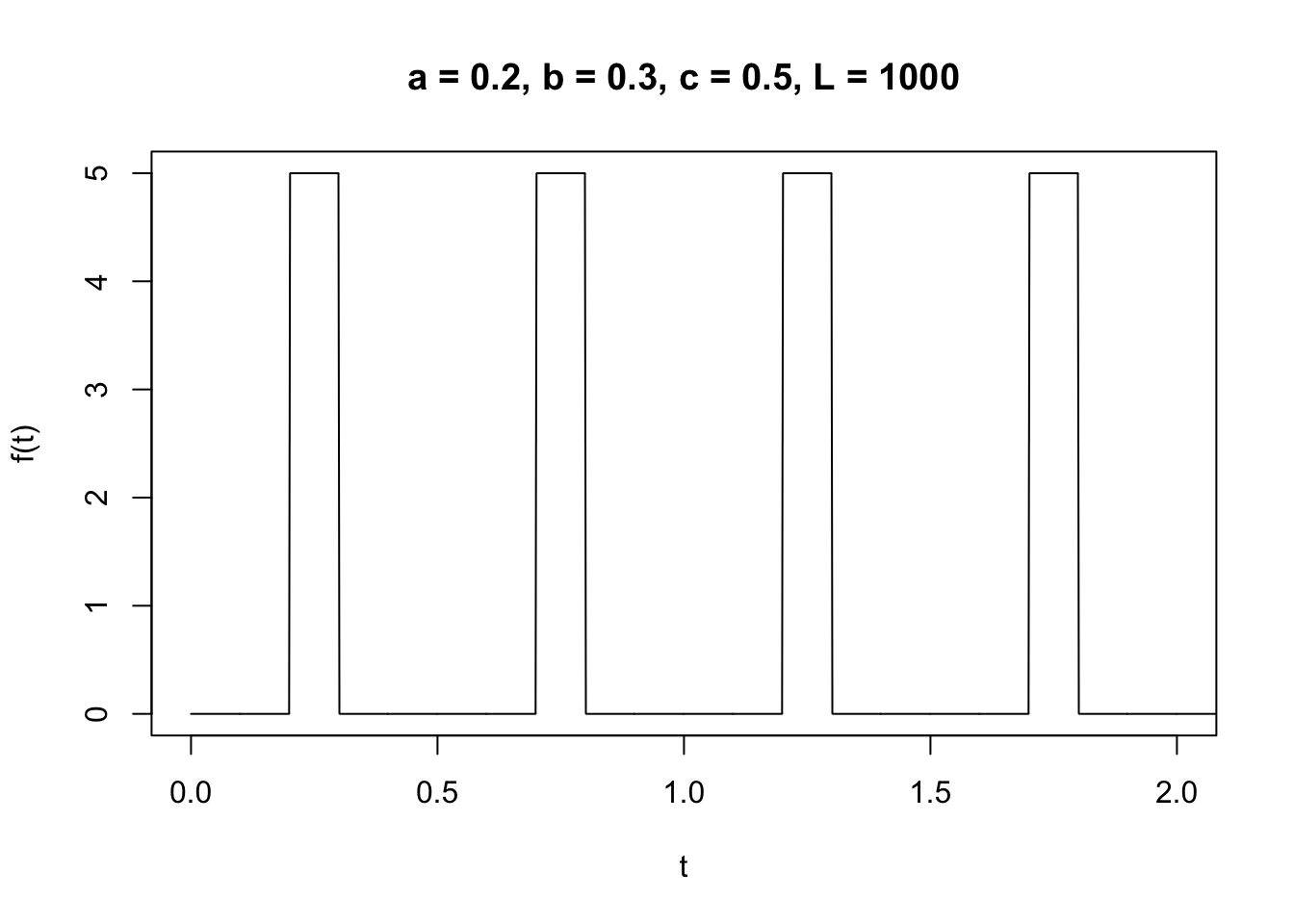
This function feeds a high-amplitude sine function through a logit, offsetting so as to have the pulse start and stop at arbitrary times. It has an integral of one per period for large \(L\).
\[f(t) = \frac{c}{a - b} \frac{1}{1 + e^{L \left(sin(2\pi((t-a)/c + \xi)) - sin(2\pi\xi)\right)} }\]
where
\[\begin{aligned} t &= \text{time} \\ a &= \text{time at start of pulse} \\ b &= \text{time at end of pulse} \\ c &= \text{period length} \\ a &< b < c \\ L &= \text{an arbitrarily large number} \\ \xi &= \frac{3}{4} - \frac{b - a}{2c} \\ \end{aligned}\]
smooth_pulse = function(time, start, stop, cycle = 1, steep = 1000) {
xi = 3/4 - (stop - start)/(2* cycle)
(cycle / (stop - start)) /
(1 + exp(steep*(sin(2*pi*((time - start)/cycle + xi)) - sin(2*pi*xi))))
}
x = seq(0,5,by=0.001)
plot(x, smooth_pulse(x, start = 0.2, stop = 0.3, cycle = 0.5), xlim = c(0,2),
type = "l", xlab = "t", ylab = "f(t)",
main = "a = 0.2, b = 0.3, c = 0.5, L = 1000")